| resources | ||
| Analityka.py | ||
| Euler.py | ||
| Main.py | ||
| Parametry.py | ||
| README.md | ||
| Wykresy.py | ||
Symulacja i analiza rzutu ukośnego
Cel projektu
Celem projektu jest stworzenie programu w Pythonie, który symuluje rzut ukośny w jednorodnym polu grawitacyjnym bez oporu powietrza. Program oblicza:
- trajektorie ruchu na podstawie dokładnego rozwiązania analitycznego,
- przybliżoną trajektorię metodą numeryczną – metodą Eulera,
- oraz porównuje obie metody, analizując dokładność w zależności od kroku czasowego
t.
Wymagania
Do uruchomienia projektu wymagane są biblioteki:
pip install numpy matplotlib
Struktura plików
Main.py– główny plik uruchamiający programAnalityka.py– obliczenia dokładne (analityczne) na podstawie wzorów fizycznychEuler.py– implementacja metody EuleraWykresy.py– rysowanie wykresów porównawczychParametry.py– definiowanie parametrów początkowych (v0, kat, h0, dt)
Uruchamianie programu
Po zainstalowaniu bibliotek, uruchom program wpisując:
python main.py
Wygenerowane wykresy
Program generuje dwa wykresy:
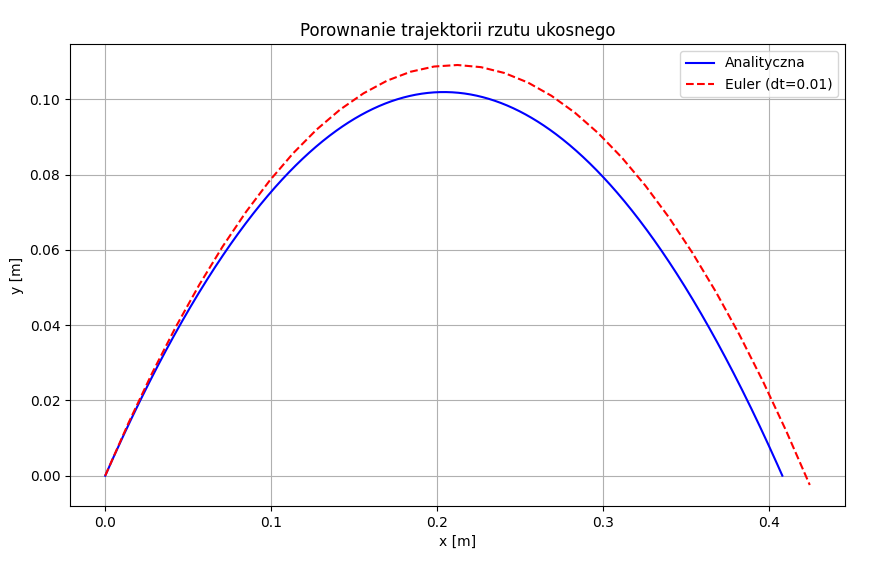
- Porównanie trajektorii analitycznej i numerycznej (Euler)
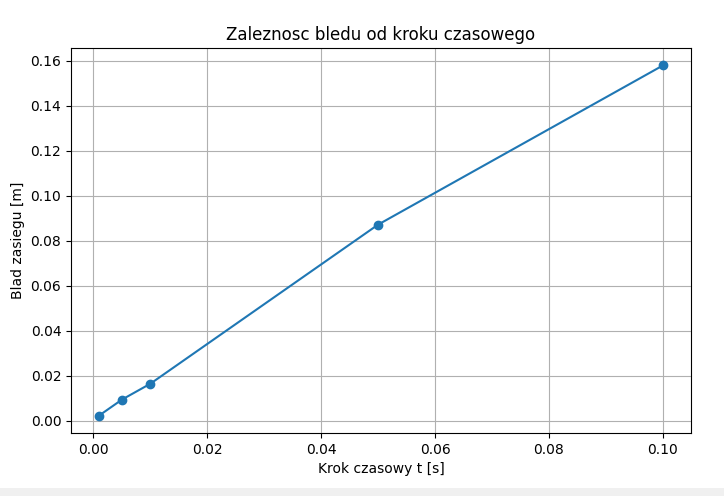
- Wykres błędu w zasięgu w zależności od wielkości kroku czasowego
t
Wykresy:
Analiza dokładności
Program analizuje, jak krok czasowy wpływa na dokładność metody Eulera:
- im mniejsze t, tym mniejszy błąd w zasięgu rzutu,
- dla zbyt dużych kroków trajektoria znacząco odbiega od wzorcowej.
Wnioski
- Metoda Eulera przy małych krokach daje zadowalającą dokładność.
- Program pokazuje, jak ważny jest wybór kroku czasowego w metodach numerycznych.
- Prosta implementacja pozwala zrozumieć podstawy całkowania numerycznego i ruchu w fizyce klasycznej.
Uwagi techniczne
- Symulacja zatrzymuje się automatycznie, gdy ciało spadnie na ziemię (y < 0).
- Dla bardzo małych t program może działać wolniej (więcej iteracji).
Autor
Patryk Zamorski